1. What is overloading?

A lot of what is said on the textbooks and on the Internet is obscure. In my own words:
C++ can have multiple definitions of functions and operators, similar to a word with multiple definitions. They are called function overloading and operator overloading.
You can use the function with the same name or the same operator to achieve different effects.

(1). Function overloading in C++

In the same scope, there can be a group of functions with the same name and different parameter lists. Their functions are similar, but their internal formal parameters must be different. We call this group of functions overloaded functions.
Role: We can reduce the number of function names by doing so and avoid the pollution of the name space. It is of great benefit to the readability of the program.

(2). Operator overloading in C++

In C++ language programs, we can redefine and overload many built-in operators, and I can implement custom functions through overloading. Overloaded operators must have functions with special names. Here we have a new keyword operator. Operator overloading must consist of the keyword operator and the operator symbol to be overloaded, and it needs a return type and a parameter list. As follows:

1
ComplexNumber operator+(ComplexNumber z);

Of course, there are also some operators defined in C++ cannot be overloaded:
The following is a list of operators that are non-overloadable:

Non-overloadable operator statement
. Member access operator
.* and ->* Member pointer access operator
:: Domain operator
sizeof Length operator
?: Conditional operator
# Preprocessing symbol

2. Knowledge of complex numbers (partial)

(1). Definition and concept of plural

A complex number is a number expressed in the form of a + bi, where a and b are real numbers, and i can be said to be the solution of the equation x^2 = -1. Since no real number satisfies this equation, it is called imaginary number. For the complex number a + bi, a is called the real part, and b is called the imaginary part. Despite the historical term “fiction”, complex numbers are regarded as “real” as real numbers in mathematical sciences, and are the basis for many aspects of scientific descriptions in nature.

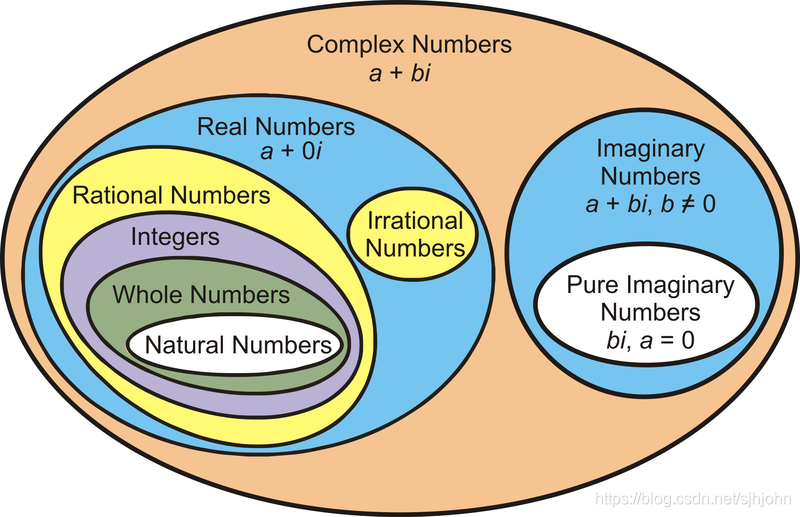
Complex numbers can solve certain equations, and these equations have no real number solutions.
For example, the equation (x+1)^2 = -9
This equation has no real number solution, because the square of a real number cannot be negative. But plurals provide a solution to this problem. It is to extend the real number with the uncertain i (sometimes called the imaginary unit) satisfying the relation i square = -1, so that the solution of the equation similar to the previous equation can be found. In this case, the solutions are -1 + 3i and -1-3i.

(2). The geometric meaning of complex numbers

Geometrically, complex numbers extend the concept of one-dimensional number lines to the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. The complex number a + bi can be identified by a point (a,   b) in the complex plane. Complex numbers with zero real numbers are called pure imaginary numbers; the points of these numbers lie on the vertical axis of the complex plane. A complex number with zero imaginary part can be regarded as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be expressed in polar coordinates, which associate each complex number with its distance from the origin (its magnitude) and a specific angle (called the argument of the complex number).

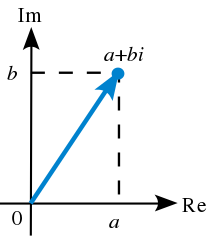
Complex numbers can be represented visually as a pair of numbers（a，  b），A vector is formed on the Argand graph, which represents a complex plane. “Re” is the real axis, “Im” is the imaginary axis, and i satisfies i^2 = -1.
Shows：
1.The complex number z=a+bi corresponds to the point (a, b) in the complex plane one to one
2. The complex number z=a+bi has a one-to-one correspondence with the vector OZ, where the coordinates of the Z point are (a, b)

(3). Addition and subtraction of complex algebraic forms

**Addition of two complex numbers:**：

$\ (x+yi)+(u+vi)=(x+u)+(y+v)i$

Two complex numbers subtraction rule：

$\ (x+yi)-(u+vi)=(x-u)+(y-v)i$

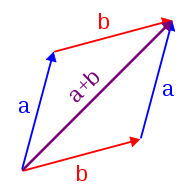
Of course, we can also understand the addition and subtraction of complex numbers through geometric forms. We can geometrically add two complex numbers by constructing parallelograms. Visualization using a complex plane: the sum of two complex numbers a and b is a point in the complex plane, which is obtained by constructing a parallelogram from three vertices O The points a and b of the arrow (provided they are not in a line). Equivalently, these points A and B are respectively called the fourth point X of the parallelogram. The triangles OAB and XBA are the same. The visualization of subtraction can be achieved by considering additional negatives.

(4). Multiplication and division of complex numbers

The rule of multiplication of complex numbers:

$\ (x+yi)*(u+vi)=(xu-yv)+(xv+yu)i$

The rule of division of complex numbers:
Here you need to use the conjugate complex number, that is, the two real parts are equal, and the imaginary parts are opposite to each other. When the imaginary part is not zero, the conjugate complex number means that the real part is equal and the imaginary part is opposite. If the imaginary part is zero, the conjugate complex number is itself. When the imaginary part is not equal to 0, it is also called conjugate imaginary number. The conjugate plural of the complex number z is denoted as z (plus a horizontal line, I can’t type this word if someone knows how to write it in a Markdown editor, can teach me), sometimes it can also be expressed as Z*. At the same time, the complex number z (plus one horizontal) is called the complex conjugate of the complex number z.

On the reciprocal calculation of non-zero complex numbers:

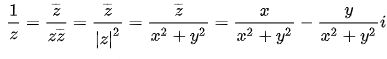
This can be used to represent the division of any complex number (z is not equal to 0)

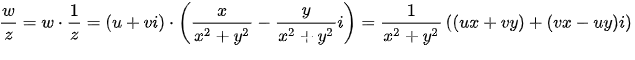
3. Friend function in C++

A friend function is a function that is not a member of a class, but it can access all members of the class. It can be understood that the class grants a privilege to the friend function, so that the friend function can easily access and utilize all private and protected members.
Of course, the concept of friend can be a function or a class. We call it Friend Function and Friend Class. Our project of the friend category is currently not in use, so I will not analyze it carefully this time.
Function: If you are a developer, you see a project from someone else in the library, and you want to practice. In many cases, you cannot access the private and protected members of the code. If the function in the class has a friend function, it means that you can access private members and protected members in this friend function.
Key word：friend
If you want to declare a function as a friend of a class, you need to use the keyword friend before the function ** in the class definition, as shown below:

1
friend ComplexNumber operator+(const float a, const ComplexNumber &z);

4. Ideas and design

(1). Program composition and ideas

For the idea of ​​the program, I first wrote a complex number class. In the private members of the class, I use double-precision floating-point numbers to define the real and imaginary parts. I will overload my own functions in public members. The real part and imaginary part can be input into the system. Here I have discussed three situations: both real and imaginary parts are input meaning; real and imaginary parts are not input; only imaginary part is input. And I initialize the real and imaginary parts to 0.
In the shared member, a function for adding real and imaginary parts is also written to realize the storage and conversion of real and imaginary parts. And the function of setting is the same. Then there is the function of the program output: internally I wrote a judgment statement to judge whether the imaginary part is greater than or equal to 0. The last is the function that overloads the four operations and the input and output operators. I will overload the addition in two cases. (It’s another matter to use class templates and so on. I will overload functions and operators here). I will set the input, output, and addition as friend functions so that they can directly access private members. Finally, write a test function statement outside the class. Just call it on the main function.

(2). Some functions correspond to the role of source code

When outputting, judge whether the imaginary part is greater than or equal to 0 to prevent negative situations such as negatives:

1
2
3
4
5
6
7
8
void ComplexNumber::Show()
{
	if(im>=0)
	cout <<"("<< re << "+" << im <<"i)";
	else
	cout <<"("<< setiosflags(ios::fixed) << setprecision(2) << re << "+" << im << "i" <<")";

};

Implementation of complex multiplication (overload of multiplication operator):

1
2
3
4
5
6
7
ComplexNumber ComplexNumber::operator *(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=re*z.re-(im*z.im);
	tmp.im=im*z.re+re*z.im;
	return tmp;
}

Implementation of complex division operation (overload of division operator):

1
2
3
4
5
6
7
ComplexNumber ComplexNumber::operator/(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=(re*z.re+im*z.im)/(z.re*z.re+z.im*z.im);
	tmp.im=(im*z.re-re*z.im)/(z.re*z.re+z.im*z.im);
	return tmp;
}

Overloading of output operators：

1
2
3
4
5
6
7
8
9
10
ostream & operator << (ostream & a,const ComplexNumber & z)
{
	if(z.re==0&&z.im==0)a << setiosflags(ios::fixed) << setprecision(0) << z.re;
	else if(z.im==0)a << setiosflags(ios::fixed) << setprecision(0) << z.re ;
	else if(z.im>0)
	a << setiosflags(ios::fixed) << setprecision(2) << z.re << "+" << z.im << "i";
	else if(z.im<0)
	a << setiosflags(ios::fixed) << setprecision(2) << z.re << z.im << "i";
	return a;
}

Test input function:

1
2
3
4
5
6
7
8
9
10
void CN() 
{ 
    //ComplexNumber
	ComplexNumber cn1, cn2;
	std::cin >> cn1 >> cn2;
	std::cout<<cn1+cn2 << std::endl;
	std::cout<<cn1 - cn2 << std::endl;
	std::cout<<cn1*cn2 << std::endl;
	std::cout<<cn1 / cn2 << std::endl;
}

(3). Overall source code

The overall source code is as follows:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <iostream>
#include <iomanip>
using namespace std;
class ComplexNumber
{
private:
	double im,re;
public:
	ComplexNumber(double i=0, double r=0);
//	ComplexNumber();
//	ComplexNumber(int i);
    ComplexNumber Add(ComplexNumber z); 
    ComplexNumber operator+(ComplexNumber z);
    friend ComplexNumber operator+(const float a, const ComplexNumber &z);
    friend istream & operator >> (istream & b, ComplexNumber &z);
    friend ostream & operator << (ostream & a,const ComplexNumber & z);
    ComplexNumber operator-(ComplexNumber z);
    ComplexNumber operator*(ComplexNumber z);
    ComplexNumber operator/(ComplexNumber z);
    double Set(double x, double y);
	void Show();
	
};
ComplexNumber::ComplexNumber(double i, double r)
{
	im=r;
	re=i;
}
/*ComplexNumber::ComplexNumber()
{
	im=0;
	re=0;
} 
ComplexNumber::ComplexNumber(int i)
{
	im=i;
	re=0;
}*/ 

void ComplexNumber::Show()
{
	if(im>=0)
	cout <<"("<< re << "+" << im <<"i)";
	else
	cout <<"("<< setiosflags(ios::fixed) << setprecision(2) << re << "+" << im << "i" <<")";

};
ComplexNumber ComplexNumber::Add(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=re+z.re;
	tmp.im=im+z.im;
	return tmp;
}
ComplexNumber ComplexNumber::operator +(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=re+z.re;
	tmp.im=im+z.im;
	return tmp;
}
ComplexNumber operator +(const float a,const ComplexNumber &z)
{
	ComplexNumber tmp;
	tmp.re=a+z.re;
	tmp.im=z.im;
	return tmp;
}
ComplexNumber ComplexNumber::operator -(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=re-z.re;
	tmp.im=im-z.im;
	return tmp;
}
ComplexNumber ComplexNumber::operator *(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=re*z.re-(im*z.im);
	tmp.im=im*z.re+re*z.im;
	return tmp;
}
ComplexNumber ComplexNumber::operator/(ComplexNumber z)
{
	ComplexNumber tmp;
	tmp.re=(re*z.re+im*z.im)/(z.re*z.re+z.im*z.im);
	tmp.im=(im*z.re-re*z.im)/(z.re*z.re+z.im*z.im);
	return tmp;
}
double ComplexNumber::Set(double x, double y)
{
	im=y;
	re=x;
	return im,re;
}
istream & operator>>(istream & b, ComplexNumber &z)
{
	b >> z.re >> z.im;
	return b;
}
ostream & operator << (ostream & a,const ComplexNumber & z)
{
	if(z.re==0&&z.im==0)a << setiosflags(ios::fixed) << setprecision(0) << z.re;
	else if(z.im==0)a << setiosflags(ios::fixed) << setprecision(0) << z.re ;
	else if(z.im>0)
	a << setiosflags(ios::fixed) << setprecision(2) << z.re << "+" << z.im << "i";
	else if(z.im<0)
	a << setiosflags(ios::fixed) << setprecision(2) << z.re << z.im << "i";
	return a;
}

void CN() 
{ 
    //ComplexNumber
	ComplexNumber cn1, cn2;
	std::cin >> cn1 >> cn2;
	std::cout<<cn1+cn2 << std::endl;
	std::cout<<cn1 - cn2 << std::endl;
	std::cout<<cn1*cn2 << std::endl;
	std::cout<<cn1 / cn2 << std::endl;
}
int main(void) 
{
	CN();
	return 0;
}

So far, “C++ language uses function overloading and operator overloading to complete complex number operations“ has been successfully implemented, thank you for reading.
This part is regarded as my study notes, which was first published on the CSDN platform and hoped to help more people. If you have any problems, I will correct them. Thank you very much for your comments and suggestions.

Copyright Notice
This article is the original content of Junhao except for the following references, and the final interpretation right belongs to the original author. If there is any infringement, please contact to delete. Without my authorization, please do not reprint it privately.

5. References

[1]. CppReference https://en.cppreference.com/w/cpp/language/operators

[2]. GeeksForGeeks https://www.geeksforgeeks.org/function-overloading-c/

[3]. Wikipedia https://en.wikipedia.org/wiki/Complex_number#Addition_and_subtraction

[4]. Runoob https://www.runoob.com/cplusplus/cpp-overloading.html

[5]. Runoob https://www.runoob.com/cplusplus/cpp-friend-functions.html

[6]. 360Doc http://www.360doc.com/content/19/0118/12/46601607_809660209.shtml